ZK programming using Arkworks
Arithmetic circuits
In the process of generating ZK-SNARKs for arbitrary computation there is one key step, called arithmetization. This is where this computation, written in some high level language like Aleo instructions, is turned into an arithmetic circuit, a graph where each node is an operation (addition, multiplication, etc) and each edge/arrow is some input or output to/from that gate. Below is an example:
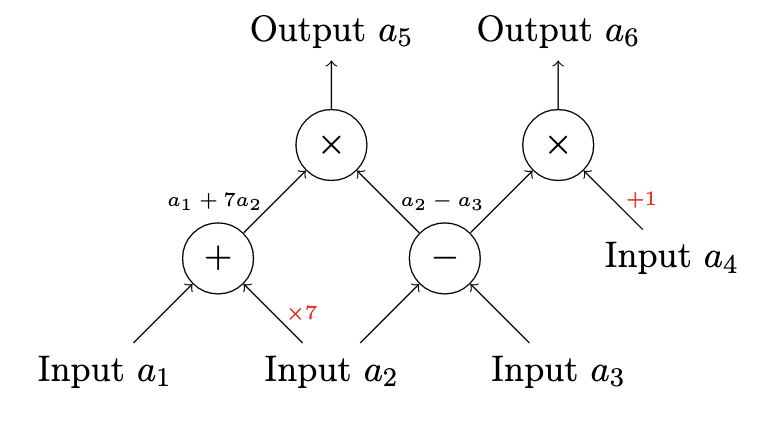
Here, the circuit has four inputs $a_1$, $a_2$, $a_3$, and $a_4$ and two outputs $a_5$ and $a_6$, that encode the following computation:
$$ a_5 = (a_1 + 7a_2) * (a_2 - a_3) \ a_6 = (a_2 - a_3) * (a_4 + 1) $$
R1CS
Arithmetic circuits can be expressed in a different but equivalent way, called a Rank One Constraint System. We're not going to go into much detail about it, but the high level idea is an R1CS is an equation of the form
$$ (\sum a_k x_k) * (\sum b_k x_k) = (\sum c_k x_k) $$
where the $x_k$ can roughly be thought of as the inputs to the circuit. More compactly, this can be written as
$$ Ax * Bx = Cx $$
for some appropriate A, B and C.
Arkworks circuits are expressed in R1CS form, so a circuit is just referred to as a constraint system or just a set of constraints.
Arkworks circuit API
Arkworks exposes an API to create circuits through the ark_r1cs_std and ark_relations packages. In Arkworks, a circuit is any struct that implements the ConstraintSynthetizer trait:
#![allow(unused)] fn main() { pub trait ConstraintSynthesizer<F: Field> { /// Drives generation of new constraints inside `cs`. fn generate_constraints(self, cs: ConstraintSystemRef<F>) -> crate::r1cs::Result<()>; } }
Because all calculations inside a circuit are done on a finite field, this trait is generic over it.
Implementing ConstraintSynthetizer amounts to implementing the function generate_constraints. To give an idea of how this works, let's go through an example.
Simple circuit
We are going to write a circuit that just takes two numbers as input and checks if they are equal. We define a struct called TestCircuit
#![allow(unused)] fn main() { #[derive(Clone)] pub struct TestCircuit { /// Private input pub a: u8, /// Private input pub b: u8, } }
As the comments suggest, circuit inputs can be either public or private. Private inputs are hidden to the verifier, i.e., after constructing a proof, the verifier does not have access to them; the proof itself proves that we know a value for it that satisfies the circuit without revealing it.
Now we need to write the constraints for this circuit:
#![allow(unused)] fn main() { use ark_r1cs_std::prelude::*; use ark_relations::r1cs::{ConstraintSynthesizer, ConstraintSystemRef, SynthesisError}; impl ConstraintSynthesizer<ark_ed_on_bls12_381::Fq> for TestCircuit { fn generate_constraints( self, cs: ConstraintSystemRef<ark_ed_on_bls12_381::Fq>, ) -> Result<(), SynthesisError> { let a = UInt8::new_witness(ark_relations::ns!(cs, "a"), || Ok(self.a))?; let b = UInt8::new_witness(ark_relations::ns!(cs, "b"), || Ok(self.b))?; a.enforce_equal(&b)?; Ok(()) } } }
For the generic F type, we are using a finite field defined in the ark_ed_on_bls12_381 crate. This is a crate implementing the bls 12-381 elliptic curve that we'll use later on for proving.
To make our lives easier for now, we are using what Arkworks calls a Gadget. These are pre-generated circuits that we can use as building blocks for coding our constraints. You can sort of think of them as a standard library for circuits. In our example, we are using the UInt8 gadget, a way of defining and manipulating unsigned 8 bit integers in this context. Later on we will be showing how to do this without gadgets, defining our constraint manually.
With the UInt8 gadget, we define two private inputs (also called witnesses) a and b, and then call the enforce_equal function between them (again, this function is provided by the gadget, we'll see below how to enforce this constraint by hand).
To instantiate a circuit and check if the constraints are satisfied for a given set of inputs, we do the following:
#![allow(unused)] fn main() { use ark_relations::r1cs::{ConstraintSynthesizer, ConstraintSystem}; let circuit = TestCircuit { a: 1, b: 1 }; let cs = ConstraintSystem::new_ref(); circuit.generate_constraints(cs.clone()).unwrap(); let is_satisfied = cs.is_satisfied().unwrap(); assert!(is_satisfied); }
Doing the same with the a and b inputs being different should fail.
Constraints without gadgets
Let's write the same TestCircuit as before, but without using the UInt8 gadget. The struct definition is the same, but now the constraints are defined as follows:
#![allow(unused)] fn main() { impl ConstraintSynthesizer<ark_ed_on_bls12_381::Fq> for TestCircuit { fn generate_constraints( self, cs: ConstraintSystemRef<ark_ed_on_bls12_381::Fq>, ) -> Result<(), SynthesisError> { let a = cs.new_witness_variable(|| { Fq::try_from(self.a).map_err(|_| SynthesisError::AssignmentMissing) })?; let b = cs.new_witness_variable(|| { Fq::try_from(self.b).map_err(|_| SynthesisError::AssignmentMissing) })?; cs.enforce_constraint(lc!(), lc!(), lc!() + (ark_ed_on_bls12_381::Fq::one(), a) - (ark_ed_on_bls12_381::Fq::one(), b))?; Ok(()) } } }
To create the two private inputs, we now use the new_witness_variable method for the ConstraintSystem we get as an argument when generating constraints. Because every calculation inside a circuit actually happens in a finite field, to create the inputs we manually cast our a and b values to be field elements. Of course, the UInt8 gadget just does the same behind the scenes (the gadget treats a u8 as an array of 8 booleans using the Boolean gadget, which in turn calls this to do the conversion).
Having created our inputs, we now manually define our constraint with the enforce_constraint function. This expects three arguments called a, b, and c, which correspond to the A, B, and C values defined in the high-level R1CS equation we talked about above. Each one of them is of type LinearCombination<F>, which is nothing more than a Vec<(F, Variable)> (variable being either a constant, public/private input or another linear combination). This is just a way of encoding a sum of the form:
$$ \sum a_k x_k $$
The $a_k$s are of type F, the $x_k$s are variables.
Going back to our example, we defined our constraint by passing a, b, and c as:
#![allow(unused)] fn main() { use ark_std::One; a = lc!() b = lc!() c = lc!() + (ark_ed_on_bls12_381::Fq::one(), a) - (ark_ed_on_bls12_381::Fq::one(), b) }
The macro lc!() is provided by Arkworks and just generates an empty linear combination, i.e., zero. For our c, we are substracting from variable
#![allow(unused)] fn main() { (ark_ed_on_bls12_381::Fq::one(), a) }
the variable
#![allow(unused)] fn main() { (ark_ed_on_bls12_381::Fq::one(), b) }
which is just a complicated way of saying a - b inside our finite field. Putting it all together, our constraint is
$$ 0 * 0 = a - b $$
a.k.a.
$$ a = b $$
Note that this is not the only way of writing this constraint, in our case we could have also defined
#![allow(unused)] fn main() { a = (ark_ed_on_bls12_381::Fq::one(), a) - (ark_ed_on_bls12_381::Fq::one(), b) b = (ark_ed_on_bls12_381::Fq::one(), 1) c = lc!() }
encoding the equation
$$ (a - b) * 1 = 0 $$
As is clear from this example, it is much easier to work with gadgets if you can, as they abstract a lot of details from the programmer.
Proving and verifying our computation with the Marlin crate
With our circuit in hand, what we need to create a ZK-SNARK over it is a proving system, a way to obtain a proof that we ran the circuit with the given inputs (both public and private) and it produced the given outputs (again, both public and private). TODO: check if outputs are actually a part of the circuit/proof API or if they are a higher level thing.
Arkworks provides packages for two different proving systems: Groth16 and Marlin. For the next example we'll be using Marlin, which Aleo uses for its blockchain.
The API for both generating and verifying proofs is incredibly simple:
#![allow(unused)] fn main() { use ark_marlin::{Marlin, SimpleHashFiatShamirRng}; use ark_bls12_381::{Bls12_381, Fr}; use ark_poly::univariate::DensePolynomial; use ark_poly_commit::marlin_pc::MarlinKZG10; use blake2::Blake2s; use rand_chacha::ChaChaRng; type MultiPC = MarlinKZG10<Bls12_381, DensePolynomial<Fr>>; type FS = SimpleHashFiatShamirRng<Blake2s, ChaChaRng>; type MarlinInst = Marlin<Fr, MultiPC, FS>; #[test] fn prove_and_verify() { let rng = &mut ark_std::test_rng(); let universal_srs = MarlinInst::universal_setup(100, 25, 300, rng).unwrap(); let circuit = super::TestCircuit { a: 1, b: 1 }; let (index_pk, index_vk) = MarlinInst::index(&universal_srs, circuit.clone()).unwrap(); let proof = MarlinInst::prove(&index_pk, circuit.clone(), rng).unwrap(); let proof_verifies : bool = MarlinInst::verify(&index_vk, &[], &proof, rng).unwrap(); assert!(proof_verifies); } }
Before going over the code, we'll cover how proofs are carried out.
In Marlin and other proving systems, generating and verifying proofs for a given circuit requires having previously sampled a proving key and a verifying key, respectively. You can think of the proving key as something that homomorphically encrypts the circuit, and the verifying key as something that allows to check whether the circuit computation is correct, without having to run it entirely or decrypt it.
The need for a proving/verifying key-pair for every circuit is an inconvenience, since in a setting like the Aleo blockchain there could be thousands of programs (which are ultimately circuits); executing or verifying any of them would require knowledge of these keys that the program's owner generated. This prompted the need for an agreed-upon, deterministic way of deriving these keys, which is the entire point of Marlin as a proving system.
In Marlin, all proving and verifying keys are deterministically derived from a so called Universal Structured Reference String (SRS), sometimes also called Common Reference String (CRS). This Universal string is generated in a Universal Setup, a scheme in which lots of different people contribute to the SRS. It's crucial that multiple people participate, since this process is essentially nothing more than sampling a (huge) random value, which the SRS is derived from. In a sense, the SRS is like a global public key for every circuit created over it, derived from some private key. Knowledge of this private key allows anyone to forge proofs at will, so it needs to be a secret to everyone in the system.
Back to our code, the first thing we do is sample a universal SRS for our system. In a context like Aleo, this would have already happened and the SRS would be a public value already known to us. The universal_setup function takes a bunch of arguments that control the maximum number of constraints and variables any circuit derived from it can have. Here we keep the values low, but in a real world scenario they would be huge.
With our SRS, we instantiate our circuit and call the index function, passing the universal_srs in addition to our circuit to derive our proving and verifying keys. The reason it's called index goes back to the Marlin paper, but it refers to the key sampling.
Having our keys, all it takes to produce a proof is calling prove passing the proving_key, our circuit and a source of randomness. To verify it, in addition to the verifying_key, our circuit and a source of randomness, we pass a list with the public inputs for the circuit. The verify function will return a Result<bool>.
Deeper dive into Marlin
In the preceding section we swept under the rug a very important part of the code, namely these three imports:
#![allow(unused)] fn main() { type MultiPC = MarlinKZG10<Bls12_381, DensePolynomial<Fr>>; type FS = SimpleHashFiatShamirRng<Blake2s, ChaChaRng>; type MarlinInst = Marlin<Fr, MultiPC, FS>; }
The Marlin struct used for proving and verifying has three generic types which have to be provided when instantiating it:
#![allow(unused)] fn main() { pub struct Marlin<F: PrimeField, PC: PolynomialCommitment<F, DensePolynomial<F>>, FS: FiatShamirRng> }
Let's explain what they are. At a high level, Marlin is composed of three distinct parts:
- A Polynomial Interactive Oracle Proof (PIOP), a way of constructing a polynomial for our proof of the computation (i.e. our circuit/R1CS) and a protocol for interactively verifying it.
- A Polynomial commitment scheme, a method for commiting to the polynomial above without revealing it to the verifier, while allowing them to prod into it a bit to convince them that it is correct.
- A source of true randomness required by the
Fiat-Shamir heuristic, which is a way of turning the interactive verification protocol defined by the PIOP into a non-interactive one. This is really important, as without it verification would require live communication between prover and verifier.
Of these three things, the Marlin struct allows us to choose different implementations of the last two. The PIOP is fixed, but the choice of polynomial commitment scheme and source of randomness for Fiat-Shamir can be chosen; that's what the PC and FS generic types are for. The F one is simply the choice of finite field, required by the PolynomialCommitment scheme choice, which uses elliptic curve cryptography underneath.
For our example, we are using polynomial commitment and Fiat-Shamir rng implementations given by Arkworks. MarlinKZG10 is a version of the popular KZG commitment scheme; other common PC choices are FRI or DARK.
Useful References
Gadgets
Gadgets are essentially libraries that give you access to common types and operations when defining circuits.
Gadgets implement the traits R1CSVar, AllocVar, EqGadget, ToBitsGadget, ToBytesGadget, and CondSelectGadget, which provide common methods used when defining circuits.
AllocVar
Lets you instantiate constant values or public/private inputs of the type implementing it on your circuit. It provides the methods new_variable, new_constant, new_input and new_witness.
R1CSVar
Provides three methods that are usually used underneath when generating constraints:
cs()returns the underlying constraint system.is_constant()is self-explanatory.value()returns the underlying value of the variable.
EqGadget
Has various methods for both checking or enforcing equality or inequality: is_eq, is_neq, enforce_equal, etc.
ToBitsGadget
Has methods to convert the type to bits. Note that "bits" here does not mean regular 8 bit integers, but rather bits inside a circuit, i.e., zeroes or ones in the underlying finite field (they are represented as Booleans, a gadget we'll talk about below). Methods include to_bits_le, to_bits_be, etc.
ToBytesGadget
Gives you the to_bytes() method to convert the type to a byte array (i.e. Vec). Once again, note that "byte" here does not mean the regular byte you're used to, but rather a byte representation in a finite field. This representation is provided by the UInt8 gadget that we'll discuss below.
CondSelectGadget
Lets you generate constraints to select between to values. There's conditionally_select(cond, true_value, false_value) (if cond is true it returns true_value, otherwise it returns false_value) and conditionally_select_power_of_two_vector(position, values) (returns an element of values whose index in represented by position. position is an array of boolean that represents an unsigned integer in big endian order). I don't know exactly where they're used for, they seem fairly low level.
Boolean
Boolean type inside a circuit/R1CS. Example:
#![allow(unused)] fn main() { use ark_r1cs_std::bits::boolean::Boolean; use ark_ed_on_bls12_381::Fq; let a = Boolean::new_input(cs, || Ok(true))?; a.enforce_equal(&Boolean::TRUE)?; let not_a = Boolean::not(&a); not_a.enforce_equal(&Boolean::FALSE)?; let result = a.and(¬_a)?; result.enforce_equal(&Boolean::TRUE)?; }
For a more interesting one, here's sample code from arkworks that enforces the validity of a given transaction.
#![allow(unused)] fn main() { // Validate that the transaction signature and amount is correct. tx.validate( &ledger_params, &sender_acc_info, &sender_pre_path, &sender_post_path, &recipient_acc_info, &recipient_pre_path, &recipient_post_path, &initial_root, &final_root, )?.enforce_equal(&Boolean::TRUE) }
The validate method is ultimately a very complex circuit using a variety of gadgets for Merkle proof and Schnorr signature verification that returns a Boolean.
This gadget is also a building block for pretty much all other types, as it's the finite field representation of a bit. This way, types like UInt8 (see below) are implemented as arrays of Booleans underneath.
UInt8
Unsigned 8 bit integer type for circuits. Example:
#![allow(unused)] fn main() { use ark_r1cs_std::bits::uint8::UInt8; let a = UInt8::new_input(cs, || Ok(1))?; let result = a.xor(&a)?; let zero = UInt8::constant(0); result.enforce_equal(&zero)?; }
As hinted above, it's important to understand that, underneath, a UInt8 is nothing more than an array of finite field elements. This has consequences for its use. For example, the verify function provided by the Marlin crate expects to be passed an array of the corresponding circuit's public inputs. Because this API is pretty low level and operations all happen in a elliptic curve over a finite field, the elements of this array are expected to be of type F: Field.
However, when defining a circuit, you will usually be using high level constructs like UInt8. If you define a public input to be of type UInt8, when verifying you are responsible for making the conversion from it to &[F]. Note that this conversion is not simply using the from function given by finite fields, i.e., if your public inputs is a UInt8 of value 1, you can't do
#![allow(unused)] fn main() { F::from(1) }
as the representation is actually
#![allow(unused)] fn main() { let one = F::from(1); let zero = F::from(0); let public_input = vec![one, zero, zero, zero, zero, zero, zero, zero] }
There's a to_bits_le method defined by the ToBitsGadget that UInt8 implements, but it gives you a Vec<Boolean<F>>, not a Vec<F>. Another extra conversion needs to be made from Boolean to F.
UInt16, UInt32, UInt64 and UInt128
Pretty self-explanatory, though they are defined through macros. Example:
#![allow(unused)] fn main() { use ark_r1cs_std::bits::uint16::UInt16; let a = UInt16::new_input(cs, || Ok(1))?; let b = UInt16::new_witness(cs, || Ok(2))?; let c = UInt16::constant(3); let result = UInt16::addmany(&[a, b]).unwrap(); result.enforce_equal(&c)?; }
addmany is an associated function (the rust equivalent of a Java static method) defined for these types. For some reason, it's not defined for UInt8. Note that the default behaviour for addmany (at least when compiling in release) is to overflow without warning. That is, the result of u16::MAX + 1 is simply 0.
Lower level cryptographic types
TODO: There's stuff for fields, elliptic curves, pairings, polynomials and polynomial evaluations.
Complex Gadgets/Merkle Tree Example
So far we've been discussing the circuit equivalent of primitive types that all programming languages support. Eventually, the need for custom types (i.e. structs) arises.
For this, let's go through an example of how this would work. The following will be taken from the MerkleTree example here. The goal is to create a circuit that, given a merkle root, leaf and a path to the leaf, decides whether the leaf belongs to the tree or not.
So we don't reinvent the wheel, we are going to use a fixed height merkle tree implementation provided by the crypto-primitives package in arkworks. This gives us a struct
#![allow(unused)] fn main() { pub struct MerkleTree<P: Config> }
where the Config is just a generic type with the hash functions used for the tree (yes, it's functions in plural, check the crypto primitives section for details on this). This struct provides us with methods to instantiate a merkle tree with
a given list of leaves:
#![allow(unused)] fn main() { /// Returns a new merkle tree. `leaves.len()` should be power of two. pub fn new<L: ToBytes>( leaf_hash_param: &LeafParam<P>, two_to_one_hash_param: &TwoToOneParam<P>, leaves: &[L], ) -> Result<Self, crate::Error> }
and to generate a merkle path for a given leaf:
#![allow(unused)] fn main() { /// Returns the authentication path from leaf at `index` to root. pub fn generate_proof(&self, index: usize) -> Result<Path<P>, crate::Error> }
For our example, this is enough. So far we have a regular merkle tree Rust struct, but what we're looking for is an arkworks circuit to generate and verify ZK proofs of inclusion for this tree. What we'll do is create a second struct to represent this circuit:
#![allow(unused)] fn main() { #[derive(Clone)] pub struct MerkleTreeVerification { // These are constants that will be embedded into the circuit pub leaf_crh_params: <LeafHash as CRH>::Parameters, pub two_to_one_crh_params: <TwoToOneHash as TwoToOneCRH>::Parameters, // These are the public inputs to the circuit. pub root: Root, pub leaf: u8, // This is the private witness to the circuit. pub authentication_path: Option<SimplePath>, } }
Don't worry too much about the leaf_crh_params and two_to_one_crh_params, they're just variables related to the hash functions being used.
If we recall the overview, to turn this struct into a circuit all we have to do is implement the generate_constraints method for the ConstraintSynthetizer trait. This pattern is a very common one throughout arkworks and it's the same one we used in the overview example, the idea is that the fields of our circuit struct are its constant, public and private inputs exposed as regular rust types.
In turn, each of these types has a corresponding R1CS equivalent, which allows creating constant, public or private inputs inside a circuit out of these regular rust types. The simplest example of this is the UInt8 gadget we've already covered; it lets you define unsigned 8 bit integers inside a circuit, which is exactly what we need for our leaf public input.
The idea behind this pattern is to give an API to users that entirely abstracts them from the circuit logic. By providing a MerkleTreeVerification struct with regular types as fields, users of the circuit don't need to know what gadgets or constraints are.
All that being said, our generate_constraints method looks like this:
#![allow(unused)] fn main() { fn generate_constraints( self, cs: ConstraintSystemRef<ConstraintF>, ) -> Result<(), SynthesisError> { // First, we allocate the public inputs let root = RootVar::new_input(ark_relations::ns!(cs, "root_var"), || Ok(&self.root))?; let leaf = UInt8::new_input(ark_relations::ns!(cs, "leaf_var"), || Ok(&self.leaf))?; // Then, we allocate the public parameters as constants: let leaf_crh_params = LeafHashParamsVar::new_constant(cs.clone(), &self.leaf_crh_params)?; let two_to_one_crh_params = TwoToOneHashParamsVar::new_constant(cs.clone(), &self.two_to_one_crh_params)?; // Finally, we allocate our path as a private witness variable: let path = SimplePathVar::new_witness(ark_relations::ns!(cs, "path_var"), || { Ok(self.authentication_path.as_ref().unwrap()) })?; let leaf_bytes = vec![leaf; 1]; let is_member = path.verify_membership( &leaf_crh_params, &two_to_one_crh_params, &root, &leaf_bytes.as_slice(), )?; is_member.enforce_equal(&Boolean::TRUE)?; Ok(()) } }
First we allocate a RootVar public input, which is the R1CS equivalent of a merkle root. This is a type provided by arkworks, which underneath implements the AllocVar trait discussed above. As a general rule, if a type ends with Var, then it's most likely the R1CS equivalent of a regular type. The value for our RootVar public input is &self.root, i.e., the root field value of our MerkleTreeVerification struct.
Next we allocate a UInt8 public input representing our leaf and the constant values for leaf_crh_params and two_to_one_crh_params. Again, we're not going to go into much detail about these two parameters, but they're provided by arkworks and are the R1CS equivalent of the parameters required by our merkle tree hash functions (see crypto primitives for more details).
Finally, we have to allocate our private input representing the merkle path, of type:
#![allow(unused)] fn main() { pub struct SimplePathVar = PathVar<crate::MerkleConfig, LeafHashGadget, TwoToOneHashGadget, ConstraintF> }
This is a gadget provided by arkworks, the R1CS equivalent of Path<P: Config>, it's a bit more complex than the other gadgets we've seen so far and it's at the crux of this entire circuit, so let's dive more into it.
As the R1CS equivalent of Path, PathVar consists of the following fields
#![allow(unused)] fn main() { pub struct PathVar<P, LeafH, TwoToOneH, ConstraintF> { /// `path[i]` is 0 (false) iff ith non-leaf node from top to bottom is left. path: Vec<Boolean<ConstraintF>>, /// `auth_path[i]` is the entry of sibling of ith non-leaf node from top to bottom. auth_path: Vec<TwoToOneH::OutputVar>, /// The sibling of leaf. leaf_sibling: LeafH::OutputVar, /// Is this leaf the right child? leaf_is_right_child: Boolean<ConstraintF>, } }
(I'm ommiting the generic type definitions to reduce visual clutter). This struct implements the AllocVar trait to be able to create public, private or constant variables by implementing the new_variable method:
#![allow(unused)] fn main() { fn new_variable<T: Borrow<Path<P>>>( cs: impl Into<Namespace<ConstraintF>>, f: impl FnOnce() -> Result<T, SynthesisError>, mode: AllocationMode, ) -> Result<Self, SynthesisError> { let ns = cs.into(); let cs = ns.cs(); f().and_then(|val| { let leaf_sibling = LeafH::OutputVar::new_variable( ark_relations::ns!(cs, "leaf_sibling"), || Ok(val.borrow().leaf_sibling_hash.clone()), mode, )?; let leaf_position_bit = Boolean::new_variable( ark_relations::ns!(cs, "leaf_position_bit"), || Ok(val.borrow().leaf_index & 1 == 1), mode, )?; let pos_list: Vec<_> = val.borrow().position_list().collect(); let path = Vec::new_variable( ark_relations::ns!(cs, "path_bits"), || Ok(&pos_list[..(pos_list.len() - 1)]), mode, )?; let auth_path = Vec::new_variable( ark_relations::ns!(cs, "auth_path_nodes"), || Ok(&val.borrow().auth_path[..]), mode, )?; Ok(PathVar { path, auth_path, leaf_sibling, leaf_is_right_child: leaf_position_bit, }) }) } }
When we called
#![allow(unused)] fn main() { SimplePathVar::new_witness(ark_relations::ns!(cs, "path_var"), || { Ok(self.authentication_path.as_ref().unwrap()) })?; }
passing our authentication_path struct (i.e., our non-R1CS merkle path) in our circuit definition above, this internally called the new_variable method, which instantiates its internal fields by using the appropriate fields in our authentication_path.
After creating a merkle path variable in our circuit, we call its verify_membership method to check that the path is correct
#![allow(unused)] fn main() { let is_member = path.verify_membership( &leaf_crh_params, &two_to_one_crh_params, &root, &leaf_bytes.as_slice(), )?; }
this returns an R1CS Boolean, so we can then add a constraint to make sure it is true:
#![allow(unused)] fn main() { is_member.enforce_equal(&Boolean::TRUE)?; }
Notice that the bulk of our MerkleTree circuit was just this gadget, which provides the R1CS API to use inside a circuit for checking merkle paths. Because it's a gadget, however, we can use it inside other circuits as part of more complex logic. For example, we could combine it with a gadget that verifies Schnorr signatures to create a circuit that takes a signed transaction updating some state in a merkle tree and checks both things: that the signature is valid and that the caller knew a leaf of the tree.
Crypto Primitives
Pedersen Hash Function/Commitment
The Pedersen hash functions are nothing more than fixing an elliptic curve point G, and then
doing
hash(x) = xG
for a given x, which is an element of a finite field. The Pedersen parameters are just the sampling of the G. Different values of G give rise to a different Pedersen Hash.
Note that there's a very important difference between popular hash functions like Keccak/SHA3 and Pedersen: the input of SHA3 is just an array of bytes of arbitrary length, and its output a fixed byte array. On the other hand, Pedersen's input has to be a finite field element (and therefore cannot be of arbitrary length) and its output is an elliptic curve element. Indeed, this is the entire point of it; it's meant to be used in the context of ZK-SNARKS/circuits, where computation is done on elliptic curves over finite fields.
The above poses a problem for Pedersen however. When using it as the underlying hash function for a Merkle Tree, one needs to take a pair of leaves or nodes and hash both to produce the next node in the tree. When using something like SHA3, what we do is hash the concatenation of the leaves/nodes, so we can use the same hash function we use to hash leaves to hash pairs of inner nodes. In the Pedersen case we can't do this, because the length of its inputs is fixed; concatenating inputs will not work.
Because of this, Pedersen is usually divided into categories called OneToOne, TwoToOne, FourToOne, etc. OneToOne takes one input and produces one output, so it's used for hashing leaves; TwoToOne takes two inputs into one output and it's used for hashing pairs of leaves/nodes, and so on.
With this in mind, let's take a look at the MerkleTree struct defined in Arkworks:
#![allow(unused)] fn main() { pub struct MerkleTree<P: Config> { /// stores the non-leaf nodes in level order. The first element is the root node. /// The ith nodes (starting at 1st) children are at indices `2*i`, `2*i+1` non_leaf_nodes: Vec<TwoToOneDigest<P>>, /// store the hash of leaf nodes from left to right leaf_nodes: Vec<LeafDigest<P>>, /// Store the two-to-one hash parameters two_to_one_hash_param: TwoToOneParam<P>, /// Store the leaf hash parameters leaf_hash_param: LeafParam<P>, /// Stores the height of the MerkleTree height: usize, } }
Here, the leaf_nodes are of type LeafDigest, which are different from the non_leaf_nodes, which are TwoToOneDigest. These are generic types that represent the output of a OneToOne and TwoToOne ZK-Friendly hash function (like Pedersen, but it could be another one), respectively.
Additionally, there are leaf_hash_param and two_to_one_hash_param fields, containing the parameters mentioned above for the OneToOne and TwoToOne hash functions, respectively.
If you're wondering, the generic type Config just contains the types of the two hash functions used:
#![allow(unused)] fn main() { pub trait Config { type LeafHash: CRH; type TwoToOneHash: TwoToOneCRH; } }
CRH stands for Collision Resistant Hash.
Pedersen Commitment
So far we have only talked about the Pedersen hash function, not the commitment. Even though one usually thinks of all hash functions as commitments themselves, cryptographers do not consider the above Pedersen hash function as one. The reason is that a commitment must satisfy two properties:
-
It must be
binding. The commiter must not be able to open the commitment at a different value than they originally commited to. Let's go through a concrete example with hash functions to explain what this means. Let's say Alice and Bob go through a guessing game, where Alice chooses a number between 1 and 10 and Bob has to guess it.To make sure Alice isn't cheating, she first hashes the number and gives the hash to Bob. Thanks to this, when the game ends and Alice reveals the number
xshe chose, Bob can check whether Alice is lying or not by hashing it. This relies on one assumption, namely, that the hash function will not give the same result for two different values ofx(this is known ascollision resistance). -
It must be
hiding. A commitment to some data should not reveal anything about it.
The Pedersen hash above is binding, as it's collision resistant, but it is not hiding. This is because the hash of the data reveals something about it, the hash itself. This might seem like a minor thing but it's actually a big deal.
Let's say we're working with a private blockchain, where a user's balance has to live on the blockchain for auditability, but needs to be private. One way to do it would be to store hashes of user balances. This way, users commit to their balance on-chain without revealing it. If we used the Pedersen hash to do this, however, we would run into a problem. People could precompute the hashes of common values and then check for them on-chain.
For instance, we could compute the hash of 0, obtaining hash(0). Then we would immediately know which users have zero balance, by just scanning for balances with the hash(0) value.
To fix this, the Pedersen commitment is introduced. It works in the same way as the hash, but in addition to doing xG, we sample another public random curve point H and then, to compute the commitment of x, we sample a random number r. Then, the pedersen commitment is
commit(x) = xG + rH
This is now hiding, as the random value r makes the result different each time we commit. In the blockchain example above, the 0 balance does not always give the same pedersen commitment, as different people will sample a different value for r. People can no longer precompute the commitment of 0, because there's no such thing as the one commitment of 0. The important bit here is that, in order for this to work, people should always use a different value for r, which is sometimes referred to as a nonce.